I implemented a recursive pathfinding algorithm. This recursive algorithm works based on a pre-set of nodes connected together. Each node has four pointers containing further direction: Top, Button, Left and Right. The recursive algorithm simply walks through each node and looking for each of these four directions one by one toward reaching its final destination; an illustration, consider the following 7 nodes: A, B, C, D, E, F, G, H.
A (Button->D, Right->B)
B (Right->C, Left->B)
C (Left->B)
D (Button->G, Right->E, Top->A)
E (Right->F, Left->D)
F (Left->E)
G (Right->H, Top->D)
H (Left->G)
These nodes when comes to an overall view will display the following figure.
A—B—C
|
D—E—F
| G—H
In this example, suppose the walker started node is Node A and wants to go to Node H as its final destination. Node A looks at its own Right, Button, Left and Top by order; its right pointed to Node B as a result he chooses to go to Node B; Node B in the same pattern chooses to go to its right, Node C. When the walker reaches node C; as its Right, Top and Button is blocked, Node C reverts back to Node B. As well node B reverts back Node A. The walker comes back to the start point again. Then Node A goes to its button node base on the order; which means it goes to Node D. Node D goes to its right Node E and then Node F. As Node F is blocked; it goes back to Node E and Node D. Afterwards, Node D chooses to go its button, Node G according to walker order. From there Node G goes to Node H. Finally, the walker reaches its final destination.
Pseudocode:
Recursive Path Finding Algorithm ArrayList findPath(GameObject currentPoint , GameObject targetPoint , ArrayList InputArrayList) { 1-Duplicate InputArrayList as tempArrayList
2-If the currentPoint equals to target Point return inputArrayList //*** End Condition found target
3-If the Right side of the currentPoint is empty goto step 4
3.1- Add currentPoint to tempArrayList //*** Call Right
3.2- tempArrayList = findPath(currentpoint.Right, targetPoint, tempArrayList);
3.3- If tempArrayList is not null return tempArrayList
4-If the Button side of the currentPoint is empty goto step 5
4.1- Add currentPoint to tempArrayList //*** Call Button
4.2- tempArrayList = findPath(currentpoint.Button, targetPoint, tempArrayList);
4.3- If tempArrayList is not null return tempArrayList
5-If the Left side of the currentPoint is empty goto step 6
5.1- Add currentPoint to tempArrayList //*** Call Left
5.2- tempArrayList = findPath(currentpoint.Left, targetPoint, tempArrayList);
5.3- If tempArrayList is not null return tempArrayList
6-If the Top side of the currentPoint is empty goto step 7
6.1- Add currentPoint to tempArrayList //*** Call Top
6.2- tempArrayList = findPath(currentpoint.Top, targetPoint, tempArrayList);
6.3- If tempArrayList is not null return tempArrayList
7-Return null;
//*** End Condition does not found target }
Note: The actual code is in C#, You can download it from this link.
Rise of the problem in the case study: As you understand this code; it has a weakness, to illustrate it; considering the following overall view of nodes, with the assumption that the start node is Node A and the final destination is Node H.
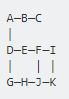
Though the best path solution is (A, D, G, H), The explained recursive pathfinding algorithm finds (A, D, E, F, I, K, J, H) as its solution; this really seems the Robot is a stupid robot :D!
Figure 1: The recursive pathfinding algorithm 
Figure 2: The recursive pathfinding algorithm with the ability to learn 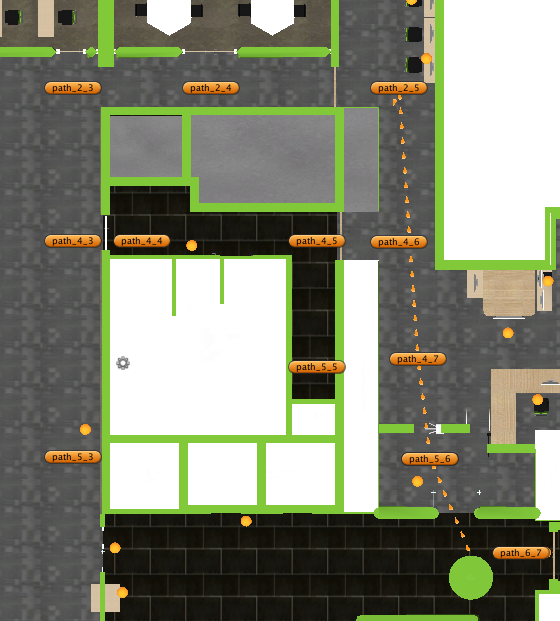
I resolved the problem by adding the learning ability for the nodes. You could see from this link the details of the issue. But, I would wonder if anybody could revise the recursive algorithm to finding the shortest path.
Thank you.