I have built a regular ANN–BP setup with one unit on the input and output layer and 4 nodes in hidden with the sigmoid. Giving it a simple task to approximate linear f(n) = n with n in range 0-100.
PROBLEM: Regardless of the number of layers, units in the hidden layer or whether or not I am using bias in node values it learns to approximate f(n) = Average(dataset) like so:
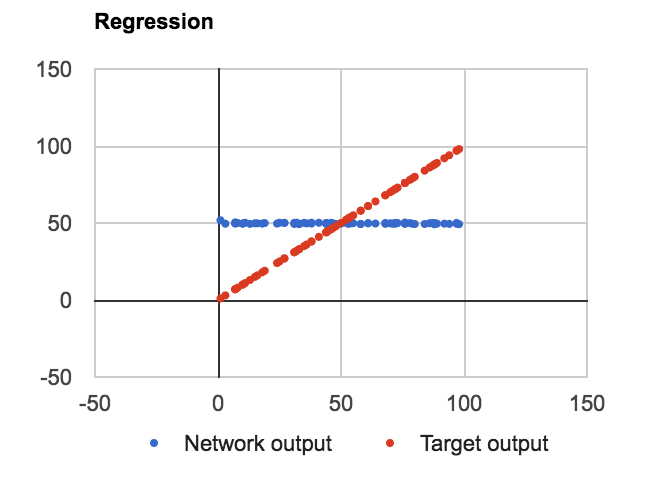
The code is written in JavaScript as a proof of concept. I have defined three classes: Net, Layer, and Connection, where Layer is an array of input, bias and output values, Connection is a 2D array of weights and delta weights. Here is the Layer code where all-important calculations happen:
Ann.Layer = function(nId, oNet, oConfig, bUseBias, aInitBiases)
{
var _oThis = this;
var _initialize = function()
{
_oThis.id = nId;
_oThis.length = oConfig.nodes;
_oThis.outputs = new Array(oConfig.nodes); _oThis.inputs = new Array(oConfig.nodes); _oThis.gradients = new Array(oConfig.nodes); _oThis.biases = new Array(oConfig.nodes); _oThis.outputs.fill(0);
_oThis.inputs.fill(0);
_oThis.biases.fill(0);
if (bUseBias) {
for (var n=0; n<oConfig.nodes;n++)
{ _oThis.biases[n] = Ann.random(aInitBiases[0], aInitBiases[1]); } } }; /****************** PUBLIC ******************/ this.id; this.length; this.inputs; this.outputs;
this.gradients;
this.biases;
this.next;
this.previous;
this.inConnection;
this.outConnection;
this.isInput = function() { return !this.previous; } this.isOutput = function() { return !this.next; } this.calculateGradients = function(aTarget) { var n, n1, nOutputError, fDerivative = Ann.Activation.Derivative[oConfig.activation]; if (this.isOutput()) { for (n=0; n<oConfig.nodes; n++) { nOutputError = this.outputs[n] - aTarget[n]; this.gradients[n] = nOutputError * fDerivative(this.outputs[n]); } }
else {
for (n=0; n<oConfig.nodes; n++)
{ nOutputError = 0.0;
for (n1=0; n1<this.outConnection.weights[n].length; n1++)
{ nOutputError += this.outConnection.weights[n][n1] * this.next.gradients[n1]; } // console.log(this.id, nOutputError, this.outputs[n], fDerivative(this.outputs[n])); this.gradients[n] = nOutputError * fDerivative(this.outputs[n]); } } } this.updateInputWeights = function() { if (!this.isInput())
{ var nY, nX, nOldDeltaWeight, nNewDeltaWeight; for (nX=0; nX<this.previous.length; nX++)
{ for (nY=0; nY<this.length; nY++)
{ nOldDeltaWeight = this.inConnection.deltaWeights[nX][nY]; nNewDeltaWeight = - oNet.learningRate * this.previous.outputs[nX] * this.gradients[nY] // Add momentum, a fraction of old delta weight + oNet.learningMomentum * nOldDeltaWeight;
if (nNewDeltaWeight == 0 && nOldDeltaWeight != 0) { console.log('Double overflow');
} this.inConnection.deltaWeights[nX][nY] = nNewDeltaWeight;
this.inConnection.weights[nX][nY] += nNewDeltaWeight; } } } }
this.updateInputBiases = function()
{ if (bUseBias && !this.isInput())
{ var n, nNewDeltaBias;
for (n=0; n<this.length; n++)
{ nNewDeltaBias = - oNet.learningRate * this.gradients[n];
this.biases[n] += nNewDeltaBias;
} } }
this.feedForward = function(a)
{ var fActivation = Ann.Activation[oConfig.activation]; this.inputs = a;
if (this.isInput()) {
this.outputs = this.inputs;
} else { for (var n=0; n<a.length; n++) { this.outputs[n] = fActivation(a[n] + this.biases[n]); } } if (!this.isOutput()) { this.outConnection.feedForward(this.outputs); } } _initialize(); }
The main feedForward and backProp functions are defined like so:
this.feedForward = function(a) { this.layers[0].feedForward(a); this.netError = 0; } this.backPropagate = function(aExample, aTarget) { this.target = aTarget; if (aExample.length != this.getInputCount()) { throw "Wrong input count in training data"; } if (aTarget.length != this.getOutputCount()) { throw "Wrong output count in training data"; } this.feedForward(aExample); _calculateNetError(aTarget); var oLayer = null, nLast = this.layers.length-1, n; for (n=nLast; n>0; n--) { if (n === nLast) { this.layers[n].calculateGradients(aTarget); } else { this.layers[n].calculateGradients(); } } for (n=nLast; n>0; n--) { this.layers[n].updateInputWeights(); this.layers[n].updateInputBiases(); } }
Connection code is rather simple:
Ann.Connection = function(oNet, oConfig, aInitWeights) { var _oThis = this; var _initialize = function() { var nX, nY, nIn, nOut; _oThis.from = oNet.layers[oConfig.from]; _oThis.to = oNet.layers[oConfig.to]; nIn = _oThis.from.length; nOut = _oThis.to.length; _oThis.weights = new Array(nIn); _oThis.deltaWeights = new Array(nIn); for (nX=0; nX<nIn; nX++) { _oThis.weights[nX] = new Array(nOut); _oThis.deltaWeights[nX] = new Array(nOut); _oThis.deltaWeights[nX].fill(0); for (nY=0; nY<nOut; nY++) { _oThis.weights[nX][nY] = Ann.random(aInitWeights[0], aInitWeights[1]); } } }; /****************** PUBLIC ******************/ this.weights; this.deltaWeights; this.from; this.to; this.feedForward = function(a) { var n, nX, nY, aOut = new Array(this.to.length); for (nY=0; nY<this.to.length; nY++) { n = 0; for (nX=0; nX<this.from.length; nX++) { n += a[nX] * this.weights[nX][nY]; } aOut[nY] = n; } this.to.feedForward(aOut); } _initialize(); }
And my activation functions and derivatives are defined like so:
Ann.Activation = { linear : function(n) { return n; }, sigma : function(n) { return 1.0 / (1.0 + Math.exp(-n)); }, tanh : function(n) { return Math.tanh(n); } } Ann.Activation.Derivative = { linear : function(n) { return 1.0; }, sigma : function(n) { return n * (1.0 - n); }, tanh : function(n) { return 1.0 - n * n; } }
And configuration JSON for the network is as follows:
var Config = { id : "Config1", learning_rate : 0.01, learning_momentum : 0, init_weight : [-1, 1], init_bias : [-1, 1], use_bias : false, layers: [ {nodes : 1}, {nodes : 4, activation : "sigma"}, {nodes : 1, activation : "linear"} ], connections: [ {from : 0, to : 1}, {from : 1, to : 2} ] }
Perhaps, your experienced eye can spot the problem with my calculations?
See example in JSFiddle